648. 单词替换
在英语中,我们有一个叫做 词根(root) 的概念,可以词根后面添加其他一些词组成另一个较长的单词——我们称这个词为 继承词(successor)。例如,词根an,跟随着单词 other(其他),可以形成新的单词 another(另一个)。
现在,给定一个由许多词根组成的词典 dictionary 和一个用空格分隔单词形成的句子 sentence。你需要将句子中的所有继承词用词根替换掉。如果继承词有许多可以形成它的词根,则用最短的词根替换它。
你需要输出替换之后的句子。
示例 1:
输入:dictionary = ["cat","bat","rat"], sentence = "the cattle was rattled by the battery"
输出:"the cat was rat by the bat"示例 2:
输入:dictionary = ["a","b","c"], sentence = "aadsfasf absbs bbab cadsfafs"
输出:"a a b c"提示:
1 <= dictionary.length <= 10001 <= dictionary[i].length <= 100dictionary[i]仅由小写字母组成。1 <= sentence.length <= 10^6sentence仅由小写字母和空格组成。sentence中单词的总量在范围[1, 1000]内。sentence中每个单词的长度在范围[1, 1000]内。sentence中单词之间由一个空格隔开。sentence没有前导或尾随空格。
思路:直接遍历即可,没有什么特别的算法,在中等题下面还是比较简单,比较考验基本功
class Solution {
public String replaceWords(List<String> dictionary, String sentence) {
ArrayList<String>res = new ArrayList<>(); //存储最终结果
String[] resource=sentence.split(" "); // 将字符串以空格分隔转为字符串数组
// 两层循环,第一层循环遍历待替换的数组;第二层循环遍历替换变量,设置一个最小长度值,因为当前的cur如果有超过一个
// 的匹配词根,需要按照词根最小替换,因此记录最小minSize,并且更新原来的替换值,temp;最后判断一下,如果temp
// 初始值没有变,证明没有匹配词根,则直接将cur加入结果res即可
for(int i=0;i<resource.length;i++){
String cur =resource[i];
int minSize = Integer.MAX_VALUE;
String temp = "";
for(int j=0;j<dictionary.size();j++){
if(cur.startsWith(dictionary.get(j))){
if(minSize>dictionary.get(j).length()){
minSize=dictionary.get(j).length();
temp=dictionary.get(j);
}
}
}
if(!temp.equals("")){
res.add(temp);
}
else{
res.add(cur);
}
}
return String.join(" ",res);
}
}设dictionary长度为m,sentence被分隔后为resource的长度为n;
时间复杂度:O(m*n)
空间复杂度 :O(n)
622. 二叉树最大宽度
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
示例 1:
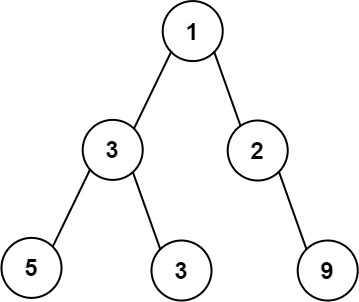
输入:root = [1,3,2,5,3,null,9]
输出:4
解释:最大宽度出现在树的第 3 层,宽度为 4 (5,3,null,9) 。示例 2:
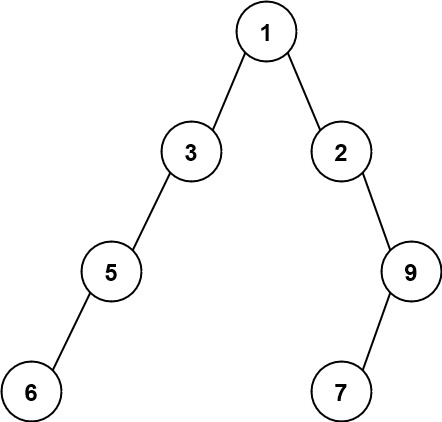
输入:root = [1,3,2,5,null,null,9,6,null,7]
输出:7
解释:最大宽度出现在树的第 4 层,宽度为 7 (6,null,null,null,null,null,7) 。示例 3:
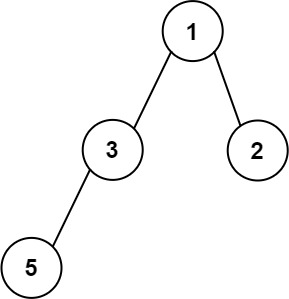
输入:root = [1,3,2,5]
输出:2
解释:最大宽度出现在树的第 2 层,宽度为 2 (3,2) 。提示:
- 树中节点的数目范围是
[1, 3000] -100 <= Node.val <= 100
思路:采用BFS遍历,统计每一层的宽度值,取其最大值为最大值。在统计每一层宽度时,只需把非null节点的位置值统计出来即可。
这里最好使用Pair<TreeNode,Integer>来保存节点及其位置,并存放在Arraylist中,如果采用Map结构,在计算每一层宽度时,需 要使用最后一个节点的位置值减去第一个节点的位置值,Map不支持随机访问,故采用List<Pair<TreeNode,Integer>>结构保存
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int widthOfBinaryTree(TreeNode root) {
if(root.left==null&&root.right==null){
return 1;
}
int result =1; // 记录结果的初始值为1
List<Pair<TreeNode,Integer>>arr = new ArrayList<>();
arr.add(new Pair<TreeNode,Integer>(root,1)); // 添加第一个根节点进arr,保证下面while循环能执行
while(!arr.isEmpty()){
List<Pair<TreeNode,Integer>>temp = new ArrayList<>(); // 设置辅助list,记录当前层的下一层节点
for(int i=0;i<arr.size();i++){
Pair<TreeNode,Integer> cur=arr.get(i);
TreeNode node = cur.getKey();
Integer pos = cur.getValue();
if(node.left!=null){
temp.add(new Pair<TreeNode,Integer>(node.left,pos*2));
}
if(node.right!=null){
temp.add(new Pair<TreeNode,Integer>(node.right,pos*2+1));
}
}
//迭代更新,注意在计算宽度时需要+1,因为位置1和位置2宽度是2,而不是2-1=1
result = Math.max(result,1+arr.get(arr.size()-1).getValue()-arr.get(0).getValue());
arr=temp;
}
return result;
}
}时间复杂度:O(n),其中 n 是二叉树的节点个数,因为需要遍历所有节点
空间复杂度:O(n),广度优先搜索的空间复杂度最多为 O(n)
思路2:DFS,深搜想起来比较复杂,没有BFS那么清晰,其实DFS和回溯很像,在本题中,如果采用访问根->访问左->访问右的方向进行,则由于这种方式会默认先访问最左边的节点,恰好我们需要的就是每一层的最左边节点的位置,即为该层位置最小值,我们这时候就记录一下,深度(用于定位我们遍历到哪一层了)和第一个节点的位置,后续遍历其他节点我们只需要统计当前节点的左节点的最大宽度和右节点的最大宽度,取值二者最大值,再与当前节点位置减去该层第一个节点位置取最大值,即
当前节点的左孩子的最大宽度,右孩子的最大宽度,当前节点位置减去该层第一个节点位置,三者取最大值即为以该节点为根节点的树的最大宽度

这道题关键点就在于我们不能直接取左孩子最大宽度和右孩子最大宽度的最大值为以该节点为根的树的最大宽度,我们还要注意对根节点的操作,如上图,如果我们以2为根节点,则还要计算该层最左边那个节点位置的距离,再与右孩子9的最大宽度和左孩子null的最大宽度(null最大宽度为0)取最大值才是2为根的树的最大宽度。
class Solution {
Map<Integer, Integer> levelMin = new HashMap<Integer, Integer>();
public int widthOfBinaryTree(TreeNode root) {
return dfs(root, 1, 1);
}
public int dfs(TreeNode node, int depth, int index) {
if (node == null) {
return 0;
}
levelMin.putIfAbsent(depth, index); // 每一层最先访问到的节点会是最左边的节点,即每一层编号的最小值
return Math.max(index - levelMin.get(depth) + 1, Math.max(dfs(node.left, depth + 1, index * 2), dfs(node.right, depth + 1, index * 2 + 1)));
}
}以上答案为官方解答,就是按照这个思路解答。
1631. 最小体力消耗路径
- 二分查找(可用于解决找出有序数组中大于指定元素的第一个元素的通用模板)
思路:通过二分枚举,枚举每一个mid值,假设mid值为到达右下角消耗的体力;如果在mid值之内能够到达右下角,则收缩mid值,进一步查找是否有更小的mid值能够到达右下角,此时right=mid-1;如果mid值之内的代价不能到达右下角,说明mid值设置太小,需要更高的代价才能到达,此时扩大mid值,即left=mid+1。最后在能够到达右下角的mid值中不断更新ans,便能找到到达右下角的最小mid值
class Solution {
int M,N;
int[][]dirs = {{-1,0},{0,1},{1,0},{0,-1}};
public int minimumEffortPath(int[][] heights) {
M=heights.length;
N=heights[0].length;
int left=0,right=999999,ans=0;//最小消耗为0,最大消耗为1000000-1=999999
while(left<=right){
int mid=(left+right)/2;
// BFS遍历
Queue<int[]>queue=new LinkedList<>();
queue.offer(new int[]{0,0});
boolean[]seen=new boolean[M*N]; //记录是否被访问过
seen[0]=true ;//0号节点被访问
while(!queue.isEmpty()){
int[]cell=queue.poll();
int x=cell[0],y=cell[1];
for(int i=0;i<4;i++){
int nx=x+dirs[i][0];
int ny=y+dirs[i][1];
if(nx>=0&&nx<M&&ny>=0&&ny<N&&!seen[getId(nx,ny)]&&Math.abs(heights[x][y]-heights[nx][ny])<=mid){
queue.offer(new int[]{nx,ny});
seen[getId(nx,ny)]=true;
}
}
}
//讨论在经历不大于mid的最大代价的情况下能否到达右下角
if(seen[M*N-1]){
// 更新ans
ans=mid;
right=mid-1;
}
else{
left=mid+1;
}
}
return ans;
}
public int getId(int x,int y){
return x*N+y;
}
}时间复杂度:O(mnlogC),其中 m 和 n 分别是地图的行数和列数,C 是格子的最大高度,在本题中 C 不超过 10^6。我们需要进行 O(logC)次二分查找,每一步查找的过程中需要使用广度优先搜索,在 O(mn)的时间判断是否可以从左上角到达右下角,因此总时间复杂度为 O(mnlogC)。
空间复杂度:O(mn),即为广度优先搜索中使用的队列需要的空间。
